Fourier’s Law Of Heat Conduction

Fourier’s Law of Heat Conduction

Fourier’s Law of Heat Conduction is a fundamental principle in the field of heat transfer, particularly in the context of conduction. Named after the French mathematician and physicist Jean-Baptiste Joseph Fourier, this law provides a quantitative description of the heat conduction process.

Table of Contents

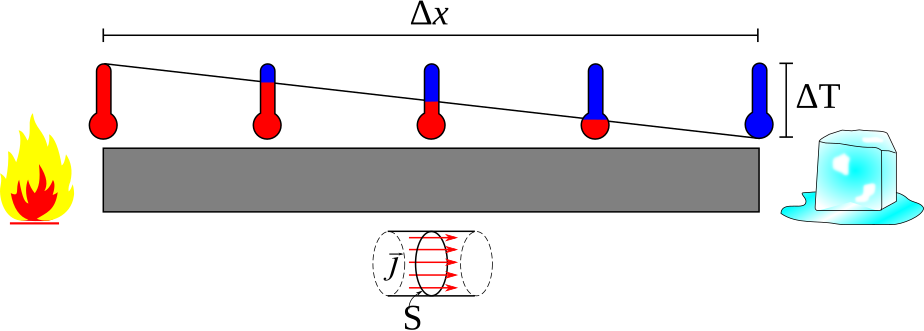
Definition of Fourier’s Law

Fourier’s Law states that the rate of heat transfer through a material is directly proportional to the negative gradient of the temperature and the area through which the heat flows. Mathematically, it can be expressed as:

q=−k∇T

where:

(q) is the heat flux (amount of heat transferred per unit area per unit time, W/m²),

(k) is the thermal conductivity of the material (W/m·K),

(∇T) is the temperature gradient (K/m).

Understanding the Components

Heat Flux (q): This represents the rate at which heat is transferred through a unit area of the material. It is measured in watts per square meter (W/m²).
Thermal Conductivity (k): This is a material-specific property that indicates how well the material conducts heat. Higher thermal conductivity means the material is a better conductor of heat. It is measured in watts per meter per Kelvin (W/m·K).
Temperature Gradient (∇T ): This is the rate of change of temperature with respect to distance within the material. It indicates how temperature varies from one point to another within the material.

One-Dimensional Form of Fourier’s Law

In one-dimensional heat conduction, Fourier’s Law can be simplified to:

qx = -k(dT/dx)

where:

( qx ) is the heat flux in the x-direction,

( dT/dx ) is the temperature gradient in the x-direction.

Integral Form of Fourier’s Law

The integral form of Fourier’s Law is used when considering the total heat transfer across a finite area and temperature difference. It is given by:

Q = -kA (delta T/ delta x)

where

( Q ) is the total heat transfer rate (W),

( A ) is the cross-sectional area through which heat is transferred (m²),

( \Delta T ) is the temperature difference between two points (K),

( \Delta x ) is the distance between the two points (m).

Derivation of Fourier’s Law

Fourier’s Law can be derived by considering a small element of material and applying the principle of conservation of energy. The rate of heat transfer through the element is proportional to the temperature difference across the element and inversely proportional to the thickness of the element.

Applications of Fourier’s Law

Fourier’s Law is widely used in various engineering applications, including:

Thermal Insulation: Designing materials and structures to minimize heat loss or gain.
Heat Exchangers: Calculating the rate of heat transfer between fluids in heat exchanger systems.
Building Design: Assessing the thermal performance of building materials and structures.
Electronic Devices: Managing heat dissipation in electronic components to prevent overheating.
Pharmaceutical Engineering: Controlling temperatures in processes such as crystallization, drying, and sterilization.

Practical Example

Consider a metal rod with a length ( L ), cross-sectional area ( A ), and thermal conductivity ( k ). If one end of the rod is maintained at a higher temperature ( T_1 ) and the other end at a lower temperature ( T_2 ), the heat transfer rate ( Q ) through the rod can be calculated using Fourier’s Law:

This equation helps in determining the amount of heat transferred through the rod over a given period.

Importance in Pharmaceutical Engineering

In pharmaceutical engineering, precise temperature control is crucial for ensuring product quality and process efficiency. Fourier’s Law helps engineers design systems that maintain optimal temperatures during various stages of drug manufacturing, such as:

Crystallization: Controlling the temperature gradient to form pure crystals.

Drying: Ensuring uniform heat distribution to remove moisture without degrading the product.

Sterilization: Achieving the necessary temperatures to eliminate microbial contamination.

Conclusion

Fourier’s Law of Heat Conduction is a cornerstone of thermal analysis in engineering. By understanding and applying this law, engineers can design efficient systems for managing heat transfer, ensuring the safety, quality, and effectiveness of various processes and products. Whether in building design, electronic cooling, or pharmaceutical manufacturing, Fourier’s Law provides the essential framework for analyzing and optimizing heat conduction.

Frequently asked questions

What is Fourier’s Law of Heat Conduction?

Fourier’s Law states that the rate of heat flow through a uniform material is proportional to the area perpendicular to the heat flow, the temperature gradient, and inversely proportional to the length of the path of flow.

How is Fourier’s Law applied in pharmaceutical engineering?

Fourier’s Law is used to design and optimize heat exchangers, which are crucial in the pharmaceutical industry for processes like sterilization, drying, and heating of materials.

What role does Fourier’s Law play in drug manufacturing?

Fourier’s Law helps in maintaining precise temperature control during drug manufacturing processes, ensuring product quality and consistency.

Can Fourier’s Law be used to improve energy efficiency in pharmaceutical plants?

Yes, by optimizing heat transfer processes using Fourier’s Law, pharmaceutical plants can reduce energy consumption and improve overall efficiency.

What are the limitations of Fourier’s Law in pharmaceutical engineering?

Fourier’s Law assumes uniform material properties and steady-state conditions, which may not always be the case in complex pharmaceutical processes.

How does Fourier’s Law impact the design of pharmaceutical equipment?

Fourier’s Law influences the design of equipment such as heat exchangers, reactors, and drying chambers by providing guidelines for efficient heat transfer.

What advancements have been made in applying Fourier’s Law to pharmaceutical engineering?

Recent advancements include the development of more accurate models and simulation tools to predict heat transfer in non-uniform and transient conditions, enhancing process design and control.